ギルバートハウス › ランダム方向ベクトルの生成

ランダム方向ベクトル

　ランダムな方向のベクトルを生成する方法とコード例です。

　以下のページの情報を参考に作成しました。

目次

△

座標変換

  • 一様乱数の組から変換してランダムな方向の平面ベクトル・3次元ベクトルを得ることができる。

平面ベクトルの場合

　平面ベクトルの場合、偏角$\theta$を一様乱数で選んで直交座標に変換する。 \begin{align} \begin{bmatrix} X \\ Y \end{bmatrix} = \begin{bmatrix} \cos \varTheta \\ \sin \varTheta \end{bmatrix} \end{align} 

/* theta ~ U(-pi, pi) */
let theta = Math.PI * (2.0 * Math.random() - 1.0);
let x = Math.cos(theta);
let y = Math.sin(theta);

3次元ベクトルの場合

　3次元ベクトルの場合には、意外なことに周辺分布が一様分布である。そこで、z成分と方位角$\varphi$を一様乱数で選んで、z成分を固定したときのベクトルのxy平面への正射影の長さが$\sqrt{1 - Z^2}$と表されることから、次のように変換する。 \begin{align} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} = \begin{bmatrix} \sqrt{1 - Z^2} \cos \varPhi \\ \sqrt{1 - Z^2} \sin \varPhi \\ Z \end{bmatrix} \end{align} 

/* z ~ U(-1, 1) */
/* phi ~ U(-pi, pi) */
let z = 2.0 * Math.random() - 1.0;
let phi = Math.PI * (2.0 * Math.random() - 1.0);
let x = Math.sqrt(1.0 - z * z) * Math.cos(phi);
let y = Math.sqrt(1.0 - z * z) * Math.sin(phi);

　下図のようにどの方向のベクトルも偏りなく実現する。

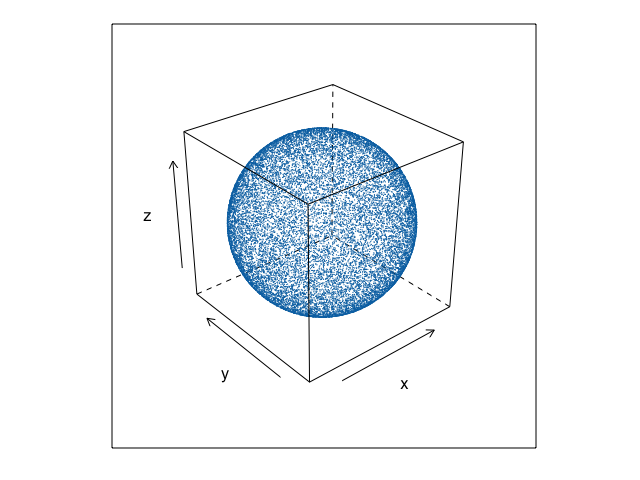
ランダム方向ベクトル

落とし穴：極角と方位角をランダムに選ぶと…

　次のよくない例では、極角$\theta$と方位角$\varphi$を一様乱数で選んで直交座標に変換している。

/* BAD EXAMPLE! */
/* theta ~ U(0, pi) */
/* phi ~ U(-pi, pi) */
let theta = Math.PI * Math.random();
let phi = Math.PI * (2.0 * Math.random() - 1.0);
let x = Math.sin(theta) * Math.cos(phi);
let y = Math.sin(theta) * Math.sin(phi);
let z = Math.cos(theta);

　下図のように(0, 0, 1)と(0, 0, −1)に近い方向のベクトルに偏ってしまう。

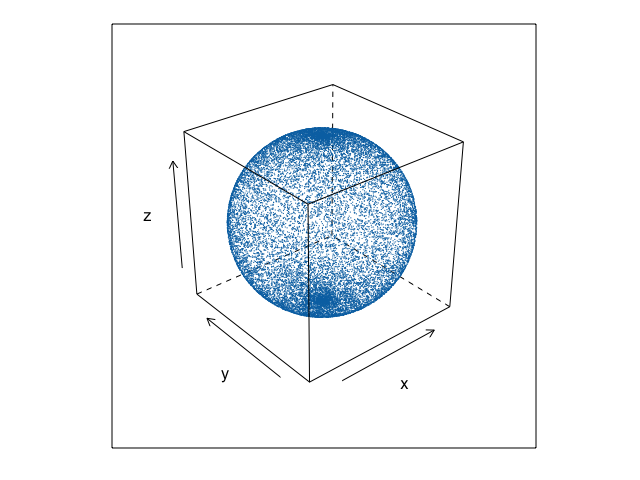
ランダム方向ベクトル（失敗例1）
△

棄却サンプリング・正規化

  • 一様乱数の組をもとに、棄却サンプリングで単位円板・球体内の一様乱数を抜き出し、これを原点からの距離で割って正規化するとランダムな方向のベクトルになる。

平面ベクトルの場合

　平面ベクトルの場合、棄却サンプリングで単位円板内の一様乱数を作り、第二段階で正規化する。

/* (u, v) ~ U_[unit-disk] */
let u, v, rr;
do {
    u = 2.0 * Math.random() - 1.0;
    v = 2.0 * Math.random() - 1.0;
    rr = u * u + v * v;
} while (rr >= 1.0 || rr == 0.0);

let s = 1.0 / Math.sqrt(rr);
let x = s * u;
let y = s * v;

3次元ベクトルの場合

　3次元ベクトルの場合も平面ベクトルの場合と同様である。

/* (u, v, w) ~ U_[unit-ball] */
let u, v, w, rr;
do {
    u = 2.0 * Math.random() - 1.0;
    v = 2.0 * Math.random() - 1.0;
    w = 2.0 * Math.random() - 1.0;
    rr = u * u + v * v + w * w;
} while (rr >= 1.0 || rr == 0.0);

let s = 1.0 / Math.sqrt(rr);
let x = s * u;
let y = s * v;
let z = s * w;

落とし穴：棄却を省略すると…

　次のよくない例では、棄却を省略して立方体内の一様乱数をそのまま正規化している。

/* BAD EXAMPLE! */
/* u ~ U(-1, 1) */
/* v ~ U(-1, 1) */
/* w ~ U(-1, 1) */
let u = 2.0 * Math.random() - 1.0;
let v = 2.0 * Math.random() - 1.0;
let w = 2.0 * Math.random() - 1.0;
let s = 1.0 / Math.sqrt(u * u + v * v + w * w);
let x = s * u;
let y = s * v;
let z = s * w;

　下図のように立方体の頂点に近い方向のベクトルに偏ってしまう。

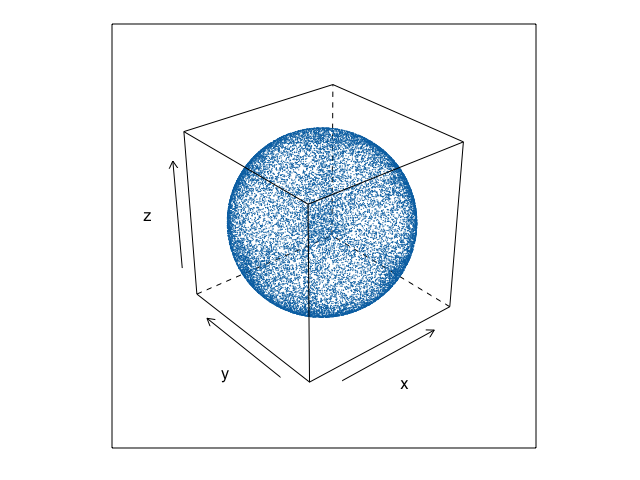
ランダム方向ベクトル（失敗例2）

落とし穴：次元が高くなると…

　棄却・正規化法では次元の呪いが発生する。$n$次元での採択率は$\frac{\pi^{n/2}}{\Gamma(n/2 + 1)} \cdot \frac{1}{2^n}$となり1,2急速に悪化する。繰り返しの期待回数（採択率の逆数）は、平面の場合に約1.3回、4次元で約3.2回、8次元で約63回、16次元では約28万回（非実用的）となる。

  1. "n-sphere § Volume and area". Wikipedia.
  2. "n次元超球の体積の求め方と考察". 高校数学の美しい物語.
採択率
△

正規乱数ベクトルを正規化

  • 標準多変量正規乱数を原点からの距離で割って正規化するとランダムな方向のベクトルになる。
  • この方法は次元の呪いの問題がなく、$n$次元ベクトルの計算量は線形にしか増えない。

3次元ベクトルの場合

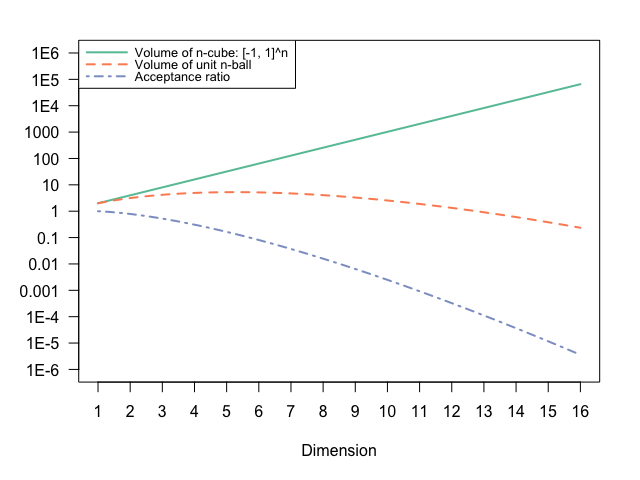
　3次元ベクトルの場合、標準3変量正規乱数を正規化する。次の例では、零ベクトル（ごく低確率）を除外して正規化している。

/* (u, v, w) ~ N(0, I_3) */
let u, v, w, rr;
do {
    u = rnorm(0.0, 1.0);
    v = rnorm(0.0, 1.0);
    w = rnorm(0.0, 1.0);
    rr = u * u + v * v + w * w;
} while (rr == 0.0);

let s = 1.0 / Math.sqrt(rr);
let x = s * u;
let y = s * v;
let z = s * w;
△

方法の選択基準

  • ランダムさの品質はどの方法でも大差ない。
  • 生成速度の面では、次元がどの程度かによって効率的な方法が変わる。大まかには以下のようになる。

平面または3次元

　座標変換法と棄却・正規化法が効率的。どちらが速いかは、三角関数のパフォーマンスと乱数生成のパフォーマンスの兼ね合いによる。正規乱数法はオーバーヘッドが大きい。

4次元以上

　正規乱数法が効率的。ただし、5次元程度までなら棄却・正規化法も選択肢に入る。（特に正規乱数生成が低速な場合。）

△
戻る