公開日：2015年4月9日
更新日：2015年4月9日
gilberthouse.math › ランベルトのW関数
ランベルトのW関数
ランベルトのW関数、またはオメガ関数、またはProduct Log関数についてのメモ。
定義と表記
関数$f(x) = xe^x$の逆関数をランベルトのW関数といい、$W(x)$で表します。
\[
y = xe^x \Longleftrightarrow x = W(y)
\]
特殊な値
- $W(-1/e) = -1$
- $W(0) = 0$
- $W(1) = \Omega$（オメガ定数：0.56714329...）
- $W(e) = 1$
正確には下の図で分かるように、$f(x) = xe^x$の単調増加区間に対応する$W_0(x)$と、単調減少区間に対応する$W_{-1}(x)$があります。
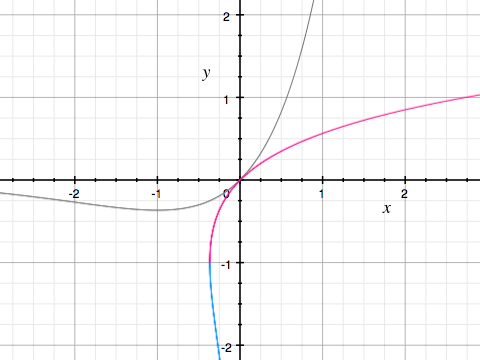
↑グレーは$y = xe^x$、ピンクは$y = W_0(x)$、ブルーは$y = W_{-1}(x)$のグラフ
方程式を解く！
超越方程式$e^{-ax} = bx + c$（ただし、$a \neq 0,\ b \neq 0$）を、$x$に対して解いてみます。
まず、$X = ax + \frac{ac}{b}$とおくと、$x = \frac{X}{a} - \frac{c}{b}$となり、これを方程式に代入。
\[
e^{-a\left(\frac{X}{a} - \frac{c}{b}\right)} = b\left(\frac{X}{a} - \frac{c}{b}\right) + c \\
\Leftrightarrow e^{-X}e^{\frac{ac}{b}} = \frac{b}{a}\,X \\
\Leftrightarrow \frac{a}{b}\,e^{\frac{ac}{b}} = Xe^{X} \\
\Leftrightarrow X = W\!\left(\frac{a}{b}\,e^{\frac{ac}{b}}\right) \\
\Leftrightarrow ax + \frac{ac}{b} = W\!\left(\frac{a}{b}\,e^{\frac{ac}{b}}\right) \\
\Leftrightarrow x = \frac{1}{a}\,W\!\left(\frac{a}{b}\,e^{\frac{ac}{b}}\right) - \frac{c}{b}
\]
関係する関数
関数$f(x) = x\log x$の逆関数を、W関数を使って表すことができます。
\[
y = x\log x \\
\Leftrightarrow e^y = x^x \\
\Leftrightarrow e^\frac{y}{x} = x \\
\Leftrightarrow \frac{y}{x}\,e^\frac{y}{x} = y \\
\Leftrightarrow \frac{y}{x} = W(y) \\
\Leftrightarrow x = \frac{y}{W(y)}
\]
よって、
\[ f^{-1}(x) = \frac{x}{W(x)} \]
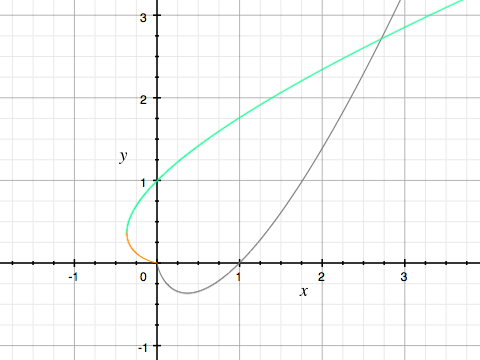
↑グレーは$y = x\log x$、グリーンは$y = x/W_0(x)$、オレンジは$y = x/W_{-1}(x)$のグラフ
例えばこんな応用
下は酵素反応におけるミカエリス‐メンテンの式です。（いきなり生物・薬学系寄りに！）
\[
v = \frac{V_{\rm max}[{\rm S}]}{K_{\rm m} + [{\rm S}]}
\]
$v$は反応速度、$[{\rm S}]$は基質濃度で、$\frac{d[{\rm S}]}{dt} = -v$の関係から、微分方程式$\frac{d[{\rm S}]}{dt} = -\frac{V_{\rm max}[{\rm S}]}{K_{\rm m} + [{\rm S}]}$が得られます。
以下、式を見やすくするため、文字を数学風に変更……。
\[
\frac{dS}{dt} = -\frac{aS(t)}{b + S(t)} \\
\Leftrightarrow \frac{b + S(t)}{S(t)}\,dS = -a\,dt \\
\Leftrightarrow \left(\frac{b}{S(t)} + 1\right)dS = -a\,dt \\
\Leftrightarrow \int\left(\frac{b}{S(t)} + 1\right)dS = -a\int dt \\
\Leftrightarrow b\log S(t) + S(t) = -at + C \\
\Leftrightarrow \log S(t) + \frac{S(t)}{b} = \frac{-at + C}{b}
\]
両辺を$e$の肩に乗せ、
\[ \Leftrightarrow S(t)\,e^{\frac{S(t)}{b}} = e^{\frac{-at + C}{b}} \\ \Leftrightarrow \frac{S(t)}{b}\,e^{\frac{S(t)}{b}} = \frac{1}{b}\,e^{\frac{-at + C}{b}} \\ \Leftrightarrow \frac{S(t)}{b} = W\!\left(\frac{1}{b}\,e^{\frac{-at + C}{b}}\right) \\ \Leftrightarrow S(t) = bW\!\left(\frac{1}{b}\,e^{\frac{-at + C}{b}}\right) \]なお積分定数は、
\[ C = b\log S(0) + S(0) \]